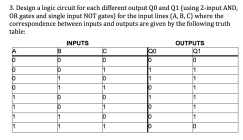
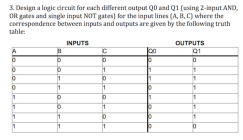
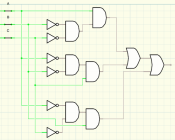
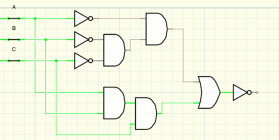
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
The Unofficial Homework Help Thread
- Thread starter LoathesRaisins
- Start date
Chinchi
Active member
So I have to write a poem/short story in the style of Edgar Allan Poe, if anyone has done this and has any ideas or possibly an attempt of their own they would let me use, it would be greatly appreciated. Also if there is infact someones I can borrow, I will sweeten the deal no doubt. Thanks guys!
LoathesRaisins
Active member
Due tomorrow?
LoathesRaisins
Active member
Not quite sure how to write this. Write the expression in simplest form : (81/4)^1/6
Brentizzle
Active member
A manufacturing firms production function is Q= KL+K+L. For this production function, MPL= K+1 and MPK = L+1. Suppose that the price r of capital services is equal to 1, and let w denote the price of the labour services. If the firm is required to produce 5 units of output, for what values of w would a cost-minimizing firm use...
a) only labour?
b) only capital?
c) both capital and labour?
I have been working on this question for the last few days with other people and its just messing with our minds. Could an Econ major please help us!!!
so far I have gotten 5/36 for a and 36/5 for b which I dont think is right.
any help would be much appreciated. I might scan another question and toss it up here if anybody can actually help with this.
THANKS!!!
a) only labour?
b) only capital?
c) both capital and labour?
I have been working on this question for the last few days with other people and its just messing with our minds. Could an Econ major please help us!!!
so far I have gotten 5/36 for a and 36/5 for b which I dont think is right.
any help would be much appreciated. I might scan another question and toss it up here if anybody can actually help with this.
THANKS!!!
Darth.Maul
Active member
I wrote a kid story once in 3rd grade. i'll upload it tomorrow
Uah
Active member
The easiest question on this assignment is turning out to be the hardest.
These are visual displays of articulatory phonetics, but I have to write the scientific\specific name they are referred to as. Please Newschoolers, you are my only hope.
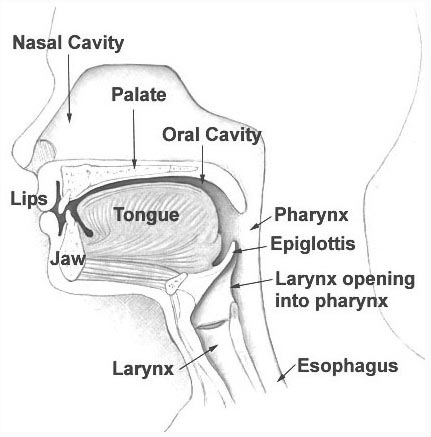
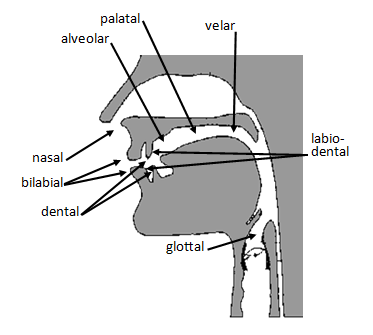
Again what are these diagrams referred to as?
Please Newschoolers you are my only hope.

These are visual displays of articulatory phonetics, but I have to write the scientific\specific name they are referred to as. Please Newschoolers, you are my only hope.

Again what are these diagrams referred to as?
Please Newschoolers you are my only hope.

.MASSHOLE.
Active member
Two quick problems. Just want to make sure I am right for the first
Consider the following system of linear equations : P=a-bq and p=c+dq. Assume that a>c>0 and that d>0, b>0. Solve for the values of p and q in terms of the parameters a, b, c, d that represent the intersection of these two lines. Note that a, b, c,d are simply positive constants
and
Suppose x^(1/4)y^(3/4)-j=0 where J is a positive constraint. Solve for dy/dx
Consider the following system of linear equations : P=a-bq and p=c+dq. Assume that a>c>0 and that d>0, b>0. Solve for the values of p and q in terms of the parameters a, b, c, d that represent the intersection of these two lines. Note that a, b, c,d are simply positive constants
and
Suppose x^(1/4)y^(3/4)-j=0 where J is a positive constraint. Solve for dy/dx
Brentizzle
Active member
damn i was just in calc last semester and we did tons of these but I totally forget everything from that pretty much. wish I could remember this and help. Could probably pull it up in my notes if you dont get it soon.
act.resist
Active member
What do you need help with, I was in an AP Spanish class in high school. I don't know if I can still recall any of it though
act.resist
Active member
Oh lol I didn't see the date
Mag
Active member
Solve for x:
3^(x+1)+3^(x+2) = 108
Simplify 3^(x+1)+3^(x+2) = 108 by making a substitution.
Simplify and substitute y = 3^x: 3^(x+1)+3^(x+2) = 12×3^x = 12 y = 108:
12 y = 108
Solve for y.
Divide both sides by 12:
y = 9
Perform back substitution on y = 9.
Substitute back for y = 3^x:
3^x = 9
Eliminate the exponential from the left hand side.
Take the logarithm base 3 of both sides:
Answer: |
| x = (2 i n pi)/(log(3))+2 for n element Z
chicken
Active member
it's probably not a typo. your teacher probably wants you to just find the integer solution which is x=2. This is how I would do it (with a bunch of extra steps for clarity)
3^{x+2}+3^{x+1}=108
3^23^x+3^13^x=108
3^x(9+3)=108
3^x=\frac{108}{12}
\log_3\left(3^x\right)=\log_3(9)
x=\log_3\left(3^2\right)
x=2
3^{x+2}+3^{x+1}=108
3^23^x+3^13^x=108
3^x(9+3)=108
3^x=\frac{108}{12}
\log_3\left(3^x\right)=\log_3(9)
x=\log_3\left(3^2\right)
x=2
chicken
Active member
that's in LaTeX.
this might work to make it more clear:
http://mathim.com/q/#3^{x+2}+3^{x+1}=108\\%0A3^23^x+3^13^x=108\\%0A3^x%289+3%29=108\\%0A3^x=\frac{108}{12}\\%0A\log_3\left%283^x\right%29=\log_3%289%29\\%0Ax=\log_3\left%283^2\right%29\\%0Ax=2
this might work to make it more clear:
http://mathim.com/q/#3^{x+2}+3^{x+1}=108\\%0A3^23^x+3^13^x=108\\%0A3^x%289+3%29=108\\%0A3^x=\frac{108}{12}\\%0A\log_3\left%283^x\right%29=\log_3%289%29\\%0Ax=\log_3\left%283^2\right%29\\%0Ax=2
DrZoidberg
Active member
Good luck with that product rule thing.
I was about to ask about some t test related but just I realized that I have 11 data so 10 degrees of freedom and my book lists that t value at 95%. Usually I never have the value I need cause I collect data in strange numbers, and I have to search around for the t value.
I was about to ask about some t test related but just I realized that I have 11 data so 10 degrees of freedom and my book lists that t value at 95%. Usually I never have the value I need cause I collect data in strange numbers, and I have to search around for the t value.
chicken
Active member
no worries. and yeah exponents and logs are very cool. Theymight seem boring at first and so does trig, but once you learn them both and about complex numbers then they lead to a very interesting mathematical relationship called euler's formula.
that's the reason the first solution that was posted here looked so crazy but you can just ignore that for now.
that's the reason the first solution that was posted here looked so crazy but you can just ignore that for now.
Arabian
Member
Line integrals are the sum of integrals over a piecewise integrable function on the set of Real numbers in counterclockwise motion using the Fundamental Theorem of Calculus v2. Curl is simply the cross product of the gradient vector (an n-dimensional vector composed of partial derivatives of their corresponding unit vectors, and surface integrals are the double integral of a vector-valued function multiplied by the square root of the partials of the x and y component values squared plus on. I can be more verbose if you like, Garret. Don't be a stranger.
Arabian
Member
When the vectors are linearly dependent, the vectors given are multiples of each other, and, therefore, have no angle between them such that the their dot products are considered simple products between numbers, rather than A . B = ABcos\Theta, as in the formal definition. Since, if the vectors were linearly independent, they may not exist on the same line, plane, space, and, thus, the existence of an angle between vectors - possibly orthogonal vectors - exists so that their sums are less than or equal to the case in which they are linearly dependent.
Benedetto.
Active member
Threads for help/provide help