Infinite Lattice of 1ohm resistors..?

St.Steezy

St.Steezy

Active member
May as well try here...

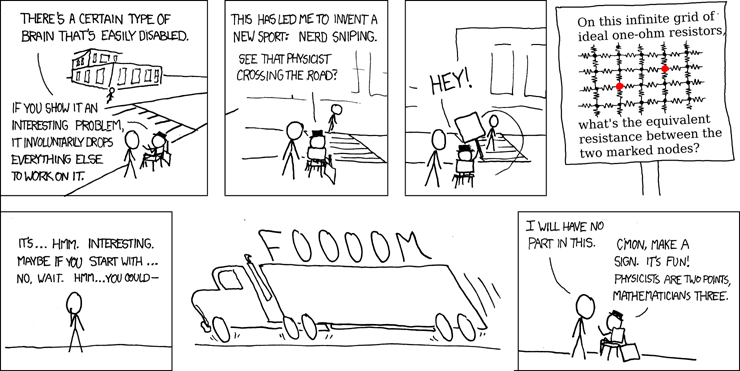
I need some help on solving the problem posed in this cartoon, http://www.xkcd.com/356/ . Its a bonus question on my assignment and I may as well give it a shot. Its probably above 99% of the math/physics comprehension of ns.. but you never know.

Cheers.
 
nerd_sniping.png
 
thats a good question, im not sure, i think there will be some sort of lower limit as the number of resistors approaches infinity. Could be 0. give me props if im right
 
i may be completely wrong but it looks like the shortest path is 3 resistors, each having R=1 ohm

R-total = R1+R2+R3 when the resistors are in series

R-total = 1+1+1 = 3 ohms

 
yeah but there are an infinite number of other pathways that the electricity could travel that would be in parallel, and thats gonna lower the resistance
 
for parellel circuits its 1/r total=1/r1 + 1/r2 + 1/r3 I believe

Id try to help you but I'm pretty sure I am in that bottom 99 percent
 
technically, the resisters are in a grid pattern, they are all the same one-ohm type. and since we cannot see where the power enters or exits the system (considering the amount of resistors is infinite), we can

a) assume there is no power source
b)seeing they are both equally placed and equally identical in resistance we can assume the difference is zero.

keep in mind I am not an electrical engineer, and I finished high-school physics last year, my hypothesis may be wrong.

use this formula,

E=IR

or 1
1/R1+1/R2+1/R3...
 
it would make sense for it to be zero because you're basically doing a limit as the number of resistors approaches infinity. which would be lim(n-->inf) 1/R which would equal zero. that just kind of looking at it by more mathmatical approach. i'm gonna have to say 0.
 
None of those are in series OR parallel because they are in a grid and have a resitor in between each one of them. For example, the horizontal resistors are not in parallel because the veritcal resistors are in between them and they are not in series for the same reason. So I don't know if that makes the resistance of the system 0 or some infinite number.
 
Tis an interesting question. My first guess was zero but I'm not sure that is correct because of the whole infinite paths thing. However, when you take limits such as that one you often find that they are not zero because the more roundabout paths for electricity have diminishing effects on the final answer. So, my answer would be just write it out, take the limit as n-> infinity and see what happens
 
Final post on this. Way more complicated than I had first thought but in the end it is a converging series, just takes a lot of effort to transform it to that. I got (4/pi)-.5 but I may be way off. Obviously though the answer must be between 0 and three so at least that number is possible.
 
that seems reasonable, also it might be that same limit you found no matter where the 2 points are im not sure
 
I'm pro, atleast 30 points..

I gave up on this problem, I don't have anytime to spare right now... and the assignment was due today.
 
This sounds right to me. If you use the parallel circuits formula and take the limit as n --> infinity that might be the best way. I really dont know though.
 
it's either infinity or zero i can't remember if resistors are 1/R or if it's R1 + R2 actually it's one.

it's one.

there's my thought process

there's an infinite number of ways to go and there's an infinite number of both ways to go parallel or in series.

the 1/R as well as R1 + R2 possibilities will add up to 1

i'm almost positive i'm right
 
You must log in or register to reply here.
Back
Top